Bài 4. Bài toán và thuật toán

1. Khái niệm bài toán

a, Khái niệm

- Bài toán là một việc nào đó mà con người muốn máy tính thực hiện

- Các yếu tố của một bài toán:

+ Input: Thông tin đã biết, thông tin đưa vào máy tính

+ Output: Thông tin cần tìm, thông tin lấy ra từ máy tính

b. Ví dụ

+ Tìm USCLN của 2 số nguyên dương

+ Tìm số lớn nhất trong 3 số nguyên dương a,b,c

+ Tìm nghiệm của phương trình bậc nhất: ax + b = 0 (a≠0)

+ ...

2. Khái niệm thuật toán

a. Khái niệm

Thuật toán để giải một bài toán là:

+ Một dãy hữu hạn các thao tác (tính dừng)

+ Các thao tác được tiến hành theo một trình tự xác định (tính xác định)

+ Sau khi thực hiện xong dãy các thao tác đó ta nhận được Output của bài toán (tính đúng đắn)

b. Cách biểu diễn thuật toán

Có 2 cách để biểu diễn thuật toán:

- Cách dùng phương pháp liệt kê: Nêu ra tuần tự các thao tác cần tiến hành

+ Ví dụ: Cho bài toán Tìm nghiệm của phương trình bậc 2: ax2 + bx + c = 0 (a≠0)?

+ Xác định bài toán

          Input: Các số thực a, b, c

          Output: Các số thực x thỏa mãn ax2 + bx + c = 0 (a≠0)

+ Thuật toán:

    Bước 1: Nhập a, b, c (a≠0)

    Bước 2: Tính Δ = b2 – 4ac

    Bước 3: Nếu Δ>0 thì phương trình có 2 nghiệm là

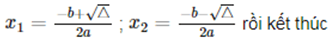
     Bước 4: Nếu Δ = 0 thì phương trình có nghiệm kép  

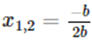
rồi kết thúc thuật toán. Nếu không chuyển sang bước tiếp theo

    Bước 5: Kết luận phương trình vô nghiệm rồi kết thúc

- Cách dùng sơ đồ khối

+ Hình thoi: thể hiện thao tác so sánh;

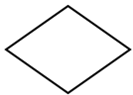
+ Hình chữ nhật: thể hiện các phép tính toán;

+ Hình ô van: thể hiện thao tác nhập, xuất dữ liệu;

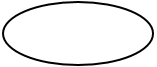
+ Các mũi tên: qui định trình tự thực hiện các thao tác.

3. Một số ví dụ về thuật toán

Bài toán 1: Kiểm tra tính nguyên tố

1. Xác định bài toán

- Input: N là một số nguyên dương

- Output:

+ N là số nguyên tố hoặc

+ N không là số nguyên tố

- Định nghĩa: "Một số nguyên dương N là số nguyên tố nếu nó chỉ có đúng hai ước là 1 và N"

- Tính chất:

+ Nếu N = 1 thì N không là số nguyên tố

+ Nếu 1 < N < 4 thì N là số nguyên tố

2. Ý tưởng

- N<4: Xem như bài toán đã được giải quyết

- N≥4: Tìm ước i đầu tiên > 1 của N

+ Nếu i < N thì N không là số nguyên tố (vì N có ít nhất 3 ước 1, i, N)

+ Nếu i = N thì N là số nguyên tố

3. Xây dựng thuật toán

a) Cách liệt kê

Bước 1: Nhập số nguyên dương N

Bước 2: Nếu N=1 thì thông báo "N không là số nguyên tố", kết thúc;

Bước 3: Nếu N<4 thì thông báo "N là số nguyên tố", kết thúc;

Bước 4: i← 2;

Bước 5: Nếu i là ước của N thì đến bước 7

Bước 6: i← i+1 rồi quay lại bước 5; ( tăng i lên 1 đơn vị)

Bước 7: Nếu i = N thì thông báo "N là số nguyên tố", ngược lại thì thông báo "N không là số nguyên tố", kết thúc;

b) Sơ đồ khối

​

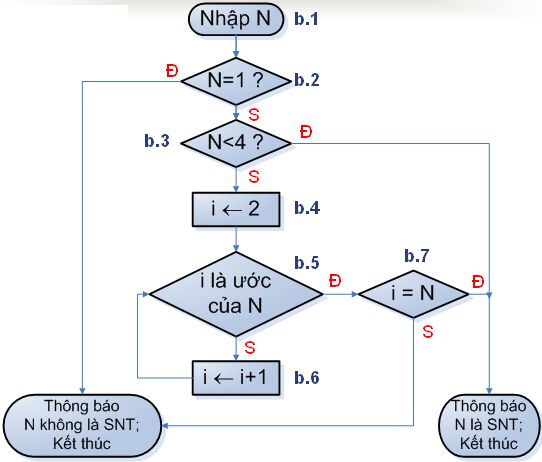
Hình 1. Sơ đồ khối thuật toán kiểm tra tính nguyên tố của một số nguyên dương N​

Lưu ý: Nếu N ≥ 4 và không có ước trong phạm vi từ 2 đến phần nguyên căn bậc 2 của N thì N là số nguyên tố

Bài toán 2: Sắp xếp bằng cách tráo đổi

1. Xác định bài toán

- Input: Dãy A gồm N số nguyên a1, a2,…,an

   Ví dụ : Dãy A gồm các số nguyên: 2 4 8 7 1 5

- Output: Dãy A được sắp xếp thành dãy không giảm

    Dãy A sau khi sắp xếp: 1 2 4 5 7 8

2. Ý tưởng

- Với mỗi cặp số hạng đứng liền kề trong dãy, nếu số trước > số sau ta đổi chỗ chúng cho nhau. (Các số lớn sẽ được đẩy dần về vị trí xác định cuối dãy)

- Việc này lặp lại nhiều lượt, mỗi lượt tiến hành nhiều lần so sánh cho đến khi không có sự đổi chỗ nào xảy ra nữa

3. Xây dựng thuật toán

- Bước 1. Nhập N, các số hạng a1, a2,…,an;

- Bước 2. Đầu tiên gọi M là số số hạng cần so sánh, vậy M sẽ chứa giá trị của N:

- Bước 3. Nếu số số hạng cần so sánh < 2 thì dãy đã được sắp xếp. Kết thúc;

- Bước 4. M chứa giá trị mới là số phép so sánh cần thực hiện trong lượt: . Gọi i là số thứ tự của mỗi lần so sánh, đầu tiên i 0;

- Bước 5. Để thực hiện lần so sánh mới, i tăng lên 1 (lần so sánh thứ i)

- Bước 6. Nếu lần so sánh thứ i> số phép so sánh M: đã hoàn tất M số phép so sánh của lượt này. Lặp lại bước 3, bắt đầu lượt kế (với số số hạng cần so sánh mới chính là M đã giảm 1 ở bước 4);

- Bước 7. So sánh 2 phần tử ở lần thứ i là ai và ai+1. Nếu ai > ai+1 thì tráo đổi 2 phần tử này;

- Bước 8. Quay lại bước 5

a) Đối chiếu, hình thành các bước liệt kê

 

b) Sơ đồ khối

​

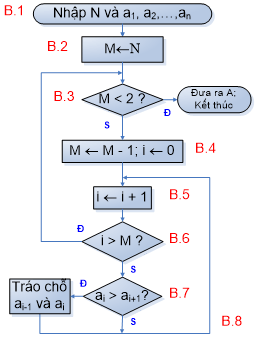
Hình 2. Sơ đồ khối thuật toán sắp xếp bằng cách tráo đổi​

Bài toán 3: Tìm kiếm tuần tự

1. Xác định bài toán

- Input : Dãy A gồm N số nguyên khác nhau a1, a2,…,an và một số nguyên k (khóa)

   Ví dụ : Dãy A gồm các số nguyên: 5 7 1 4 2 9 8 11 25 51 . Và k = 2 (k = 6)

- Output: Vị trí i mà ai = k hoặc thông báo không tìm thấy k trong dãy. Vị trí của 2 trong dãy là 5 (không tìm thấy 6)

2. Ý tưởng

Tìm kiếm tuần tự được thực hiện một cách tự nhiên: Lần lượt đi từ số hạng thứ nhất, ta so sánh giá trị số hạng đang xét với khóa cho đến khi gặp một số hạng bằng khóa hoặc dãy đã được xét hết mà không tìm thấy giá trị của khóa trên dãy.

3. Xây dựng thuật toán

a) Cách liệt kê

Bước 1: Nhập N, các số hạng a1, a2,…, aN và giá trị khoá k;

Bước 2: i ← 1;

Bước 3: Nếu ai = k thì thông báo chỉ số i, rồi kết thúc;

Bước 4: i ← i+1

Bước 5: Nếu i > N thì thông báo dãy A không có số hạng nào có giá trị bằng k, rồi kết thúc;

Bước 6: Quay lại bước 3;

b) Sơ đồ khối
 

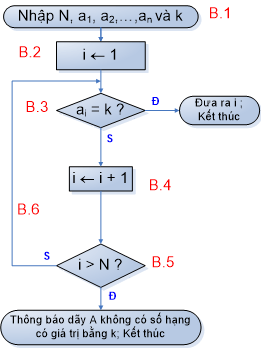
Hình 3. Sơ đồ khối thuật toán tìm kiếm tuần tự​

Bài toán 4: Tìm kiếm nhị phân

1. Xác định bài toán

- Input: Dãy A là dãy tăng gồm N số nguyên khác nhau a1, a2,…,an và một số nguyên k.

   Ví dụ: Dãy A gồm các số nguyên: 2 4 5 6 9 21 22 30 31 33. Và k = 21 (k = 25)

- Output : Vị trí i mà ai = k hoặc thông báo không tìm thấy k trong dãy. Vị trí của 21 trong dãy là 6 (không tìm thấy 25)

2. Ý tưởng

- Sử dụng tính chất dãy A đã sắp xếp tăng, ta tìm cách thu hẹp nhanh vùng tìm kiếm bằng cách so sánh k với số hạng ở giữa phạm vi tìm kiếm (agiữa), khi đó chỉ xảy ra một trong ba trường hợp:

+ Nếu agiữa= k thì tìm được chỉ số, kết thúc;

+ Nếu agiữa > k thì việc tìm kiếm thu hẹp chỉ xét từ ađầu (phạm vi) → agiữa - 1;

+ Nếu agiữa < k việc tìm kiếm thu hẹp chỉ xét từ agiữa + 1 → acuối (phạm vi).

- Quá trình trên được lặp lại cho đến khi tìm thấy khóa k trên dãy A hoặc phạm vi tìm kiếm bằng rỗng.

3. Xây dựng thuật toán

a) Cách liệt kê

b) Sơ đồ khối

​

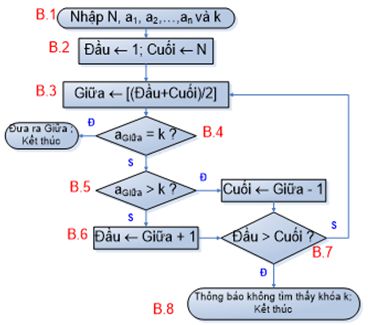
Hình 4. Sơ đồ khối thuật toán tìm kiếm tuần tự​

Nguồn: toploigiai.vn

ĐỌC THÊM

“Bất kì một chương trình máy tính nào cũng cần thuật toán/ giải thuật (algorithms). Không thuật toán, không chương trình nào hết!”

Câu nói đánh giá vô cùng đúng về vai trò cũng như giá trị của thuật toán/giải thuật đối với mỗi lập trình viên. Vậy thuật toán là gì? Tại sao thuật toán lại quan trọng như vậy? Chúng ta nên học thuật toán từ những nguồn nào là tốt nhất?,… Những thắc mắc này của bạn sẽ có ngay đáp án sau khi bạn đọc xong bài viết này.

Let’s go!

Thuật toán là gì?

Thuật toán (algorithms) có thể hiểu đơn giản là tập hợp các bước để hoàn thành một nhiệm vụ. Một số ví dụ rất cơ bản về thuật toán xung quanh bạn như: bạn có thể có một thuật toán để đi từ nhà đến trường, để làm bánh mỳ xá xíu thật ngon hoặc một thuật toán để tìm thấy những gì bạn tìm kiếm trong một cửa hàng tạp hóa nhanh nhất.

Trong khoa học máy tính khái niệm này cũng tương tự như vậy, thuật toán là một tập hợp các bước để chương trình máy tính hoàn thành một nhiệm vụ.

Tại sao thuật toán lại quan trọng với lập trình viên như vậy?

Câu trả lời rất đơn giản, học thuật toán giúp chúng ta giải quyết vấn đề một cách tốt hơn, nâng cao tư duy lập trình.

Như ví dụ mình đã nêu ở trên bạn có thể thấy rằng thuật toán ở khắp nơi quanh ta từ những vấn đề nhỏ tới vấn đề lớn. Chính vì thế thuật toán thì cũng có thuật toán đơn giản và thuật toán phức tạp.

Một số lĩnh vực trong lập trình chỉ cần những thuật toán đơn giản những cũng có những lĩnh vực cần sử dụng rất nhiều thuật toán phức tạp như: render đồ hoạ, mã hoá dữ liệu, driver, machine learning, data mining. Phải nắm vững các thuật toán này thì bạn mới có thể làm việc trong lĩnh vực đó.

Đối với mỗi lập trình viên việc giỏi thuật toán cũng giúp bạn tìm ra hướng giải quyết vấn đề nhanh hơn, viết code mạch lạc hơn. Nắm vững thuật toán, cấu trúc dữ liệu, bạn sẽ ước tính được độ phức tạp của code, đánh giá code chạy nhanh hay chậm, có scalable hay không.

Trích lời trong bài viết Thuật toán là gì? Học thuật toán làm quái gì?, có thể khẳng định thế này:

“Có một sự thật rằng, đa phần các sản phẩm phần mềm ngày nay thành công mà không cần hay sử dụng rất ít thuật toán bên trong nó. Tuy nhiên những sản phẩm có hàm lượng thuật toán cao, trí tuệ lớn, thật sự tạo ra sự khác biệt và thành công lớn hơn những sản phẩm bình thường. Sản phẩm như Google thành công vì có thuật toán tìm kiếm mạnh mẽ bậc nhất thế giới. Sản phẩm như Facebook hay Youtube cũng phải sử dụng nhiều thuật toán như tìm kiếm, gợi ý người dùng, gợi ý nội dung, … Nhưng thuật toán lại không phải yếu tố cốt lõi quyết định thành công của sản phẩm này. Do đó, việc học thuật toán, sự quan trọng của thuật toán phụ thuộc vào sản phẩm, ứng dụng mà bạn làm. Dù có giỏi hay không giỏi thuật toán, bạn vẫn có thể thành công nếu vận dụng đúng kỹ năng, hiểu biết của mình vào lĩnh vực mà bạn làm. Cá nhân tôi luôn khuyên và nhắn nhủ các bạn lập trình viên hãy luôn học và rèn luyện thuật toán. Với tôi, thuật toán giúp bạn rèn luyện tư duy giải quyết vấn đề, cùng với suy nghĩ về việc luôn tối ưu và làm sản phẩm một cách tối ưu và tổng quát. Có những lúc, thực sự bế tắc trong công việc (không chỉ là lập trình), tôi vẫn thường vào làm 1 số bài tập thuật toán để khai thông và thúc đẩy sự suy nghĩ. Sau đó tôi thấy mình minh mẫn và giải quyết công việc cũ 1 cách thuận lợi hơn.”